 Normalverteilung - Binomialverteilung
Normalverteilung - Binomialverteilung
Lernziele
- Kennenlernen der Normalverteilung und ihrer Parameter (Erwartungswert (Mittelwert) und Varianz).
- Kennenlernen der Binomialverteilung und ihrer Parameter (Anzahl Versuche n und Bernoulli-Parameter p).
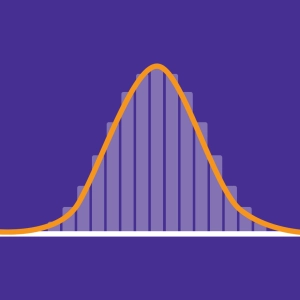
- Aufzeigen, dass sich die Binomialverteilung wie eine Normalverteilung verhält, wenn die Anzahl an Versuchen erhöht wird (Satz von Moivre-Laplace).
Die Normalverteilung beschreibt eine Wahrscheinlichkeitsverteilung vieler einzelner Werte um einen gemeinsamen Mittelwert. Die Mehrheit der Werte befindet sich nahe des Mittelwerts, während die Anzahl der Werte mit zunehmender Entfernung verringert. Diese Normalverteilung bildet eine Kure mit Glockenform, welche auch als Gauß-Kurve bzw. Gauß-Glocke bezeichnet wird.
Viele Prozesse in der Natur, der Wirtschaft und der Physik lassen sich durch die Normalverteilung gut beschreiben oder annähern.
Auch wenn sehr viele Wahrscheinlichkeitsgesetze existieren, folgt ein zufällig auftretendes Phänomen, welches häufig wiederholt wird, einer Wahrscheinlichkeitsverteilung, die auf die Normalverteilung zurückgeführt werden kann. Diese Theorie wird durch die Binomialverteilung beschrieben.
Veränderen Sie die Parameter mit Hilfe der Schieberegler. Klicken Sie auf die Grenzwerte a und b und verschieben Sie sie.

EduMedia kostenlos entdecken
Die interaktive Enzyklopädie, die Wissenschaft und Mathematik im Unterricht zum Leben erweckt.
Mehr als 1000 Ressourcen





