Fonction polynomiale (n≤2)
Une fonction polynomiale du second degré de la variable x est une somme de 3 termes algébriques, l'un d'eux contient une puissance d'ordre 2 de x.
Son expression générale s'écrit sous la forme : a.x2 + b.x + c,
a, b et c sont les paramètres de la fonction. c est l'ordonnée à l'origine de f(x) : f(0) = c.
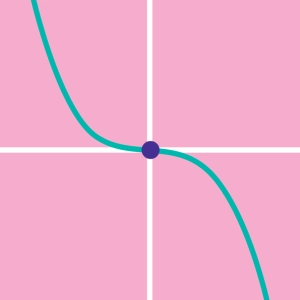
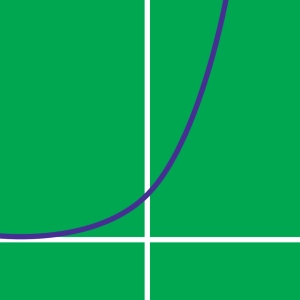
- Si a est non nul, la fonction est quadratique. Sa représentation graphique est une forme en U si a > 0 ou en U inversé si a < 0. f(x) peut s'exprimer en fonction des coordonnées de son sommet (h,k), c'est la forme canonique : f(x) = a.(x - h)2 + k. Si f(x) coupe l'axe des abscisses, la fonction possède deux zéros z₁ et z₂ : f(z₁) = f(z₂) = 0. f(x) peut s'exprimer en fonction de ses zéros, c'est la forme factorisée : f(x) = a (x - z₁)(x - z₂).
- Si a est nul, la fonction est affine ou linéaire. Son expression devient : f(x) = b.x + c. Sa représentation graphique est une droite, b est la pente de la droite.
Cette animation permet de comprendre l'influence de chaque paramètre sur la forme et l'expression de la fonction.
