Fonction exponentielle

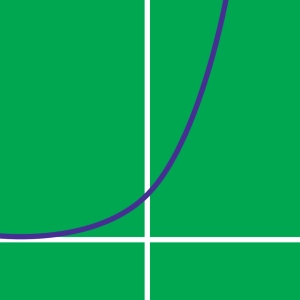
La fonction exponentielle est une fonction puissance où la variable x est l'exposant. Dans sa forme de base, la fonction exponentielle s'écrit f(x) = q^x ou f(x) = exp_q(x).

Le paramètre q est la base de l'exponentielle, c'est un réel strictement positif et différent de 1.

La variation de la fonction exponentielle s'étudie sur deux intervalles :

• 0 < q < 1 : la fonction est strictement décroissante :  f(x) → +∞ quand x → −∞ et f(x) → 0 quand x → +∞.
• q > 1 : la fonction est strictement croissante. f(x) → 0 quand x → −∞. et f(x) → +∞ quand x → 0.

Si q = 1, alors la fonction est constante. C'est la droite d'équation y = 1.

Si q ≠ 1, la fonction exponentielle a pour asymptote la droite d'équation y = 0.

La fonction exponentielle exp_q(x) est une fonction convexe qui passe par le point de coordonnées (0 , 1) : ∀ q, q⁰ = 1.

Cas particulier : La fonction exponentielle qui admet pour tangente au point (0 , 1) la droite d'équation y = x, est la fonction exponentielle de base e. Elle se note f(x) = e^x ou f(x) = exp(x). 

e est un nombre irrationnel, nommé nombre d'Euler ou nombre de Néper : e ≈ 2,718  281 : e = f(1).