Polynomiale functie (n≤2)
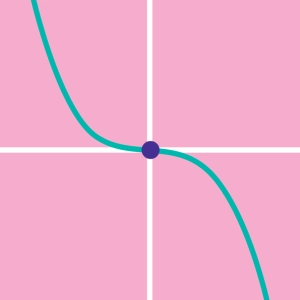
Een polynomiale functie van graad 2 wordt ook wel een kwadratische functie genoemd. De grafiek is een parabool waarvan de symmetrieas evenwijdig is aan de y-as
De algemene uitdrukking is van de vorm f(x) = ax2 + bx + c.
a, b en c zijn de parameters van de functie waarbij c de hoogte van de parabool is (waar deze de y-as snijdt). f(0) = c.
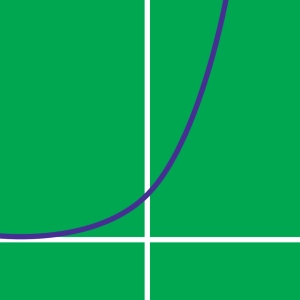
- Als a niet nul is, is de functie kwadratisch. De grafische representatie is een U-vorm als a > 0 en een omgekeerde U-vorm als a < 0. f(x) kan worden geschreven als een functie van de coördinaten van zijn top (h, k), het is de kanonieke vorm, f(x) = a(x - h)2 k. Als f(x) de x-as snijdt, dan heeft de functie twee nulpunten, z1 en z2, f(z1) = f(z2) = 0. f(x) kan worden geschreven als functie van zijn nulpunten, het is de gefactoriseerde vorm: f(x) = a(x - z1)(x - z2).
- Als a = 0, is de functie affien of lineair. De uitdrukking wordt: f(x) = bx + c. De grafische representatie is een techte, b is de helling van de rechte.
Deze animatie helpt bij het begrijpen van de invloed van elke parameter op de vorm en grafiek van de functie.
