 Translation (video)
Translation (video)
A translation is a geometric transformation that slides all points of an object in the same direction.
It is characterized by a direction (…) and a distance (…) represented by the arrow T (…) sometimes called “vector T” by mathematicians.
Let’s plot a coordinate plane and write T(a,b) the translation of “a” units in the x-direction and “b” units in the y-direction.
If point M has coordinates (x, y), then the image of M under the translation T(a,b) will be the point M’ with coordinates (x+a , y+b);
If “a” is a positive value, point M is shifted “a” units to the right, in the positive direction of x axis .
If “a” is a negative value, point M is shifted to the left, in the opposite direction.
If “b” is a positive value, point M is shifted “b” units upward, in the positive direction of y-axis
If “b” is a negative value, M is shifted “b” units downward.
If we want to find out what is the translated image of a shape under translation T(a,b), the easiest way consists in applying the transformation to each point of the shape.
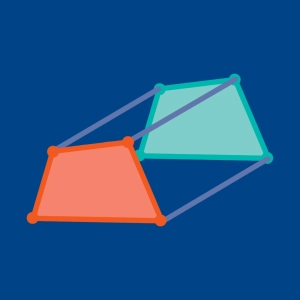
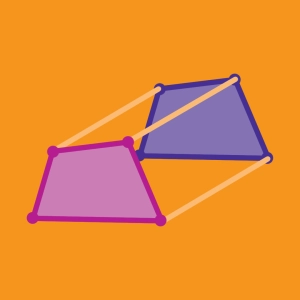
Let’s plot the image of quadrilateral ABCD under translation T(4,2)
We understand that at the end, we should see the whole shape has been moved 4 units to the right and 2 units up.
Let’s translate the first vertex A with coordinates (-3, 3).
According to the properties of the translation, we know that x-value of “A’ ” is x-value of A increased by 4, which leads to -3 + 4 = 1.
The same way there is the y-value of A’ equals y-value of A increased by 2 : 3 + 2 =5.
(…)
The same transformation is applied to the 3 other vertices. The image of quadrilateral ABCD is obtained by tracing the line segments joining the vertices A’B’C’D’.
(…)
Side AB is parallel to side A’B’ and both have the same length.
Since it is the same for all sides, the pre-image ABCD and the image A’B’C’D’ have the same perimeter and area.

Discover EduMedia for free
The interactive encyclopedia that brings science and math to life in the classroom.
Over 1,000 resources