Squeeze theorem

Learning objectives

To know how to state and apply the squeeze theorem in order to study the limit of a function at infinity.
To know how to state and apply the limit comparison theorem to explore the limit of a function at infinity.

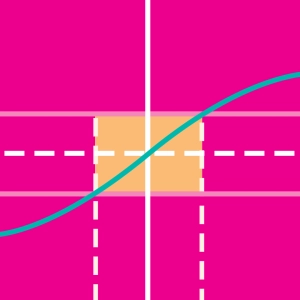
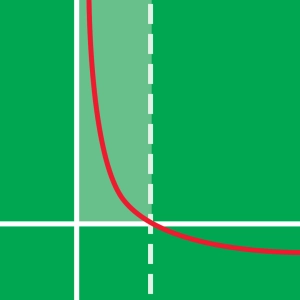
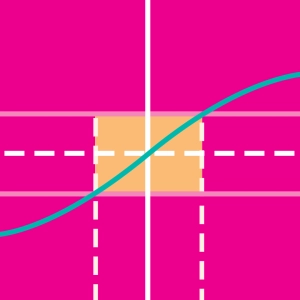
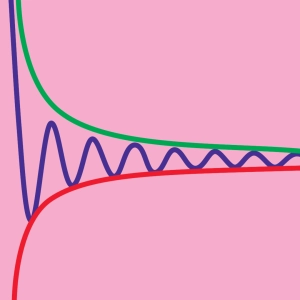
The limit at +∞ or -∞ of a continuous function on a real interval, I, can be determined by comparison with two other functions whose limit is easily calculated.

This animation provides an illustration of the squeeze theorem (also known as the pinching or sandwich theorem).

Click on the screen to freeze the points.