 Zwart lichaam
Zwart lichaam
Learning objectives
- De theoretische kromme van de wet van Planck laten zien.
- Laten zien hoe de temperatuur van invloed is op theoretische krommen.
- Torlichten dat de zwartelichaamskromme bij 3 Kelvin (fossiele straling) een getuigenis van de oerknal is.
Ieder verwarmd lichaam zendt straling uit. De klassieke natuurkunde kon het waargenomen emissiespectrum voor een theoretisch model, het zogeheten "zwarte lichaam", niet verklaren.
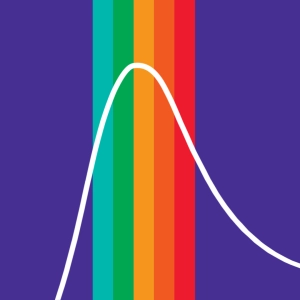
Een zwart lichaam is een ideaal object in thermodynamisch evenwicht met zijn omgeving dat zich gedraagt als een volmaakte "stralingsabsorbeerder" (alle invallende straling wordt geabsorbeerd en dus is er noch weerkaatsing noch transmissie, wat verklaart waarom een dergelijk lichaam voor ons zwart lijkt). Om in thermodynamisch evenwicht te blijven zendt het aldus verwarmde zwarte lichaam elektromagnetische straling uit in alle golflengten. De uitgestraalde energie per tijdseenheid, de luminantie, of vermogen per oppervlakte-eenheid, dekt alle golflengten en hangt uitsluitend af van de oppervlaktetemperatuur van het lichaam, zoals getoond door de krommen van de animatie.
Het was Max Planck die, in 1900, zijn beroemde vergelijking formuleerde die de wet beschreef die nu zijn naam draagt: de wet van Planck.
Zijn werk valideert de sindsdien opgekomen theorieën van de kwantummechanica. Voor het verklaren van het macroscopisch gedrag van een zwart lichaam gaat hij ervan uit dat de atomen van het zwarte lichaam in interactie zijn met elektromagnetische straling op een discrete (discontinue) manier. Lichtenergie wordt geabsorbeerd (en uitgezonden) in de vorm van energiepakketten (de kwanta). De ogenschijnlijk continue luminantie is in feite het statistische resultaat van de som van de afzonderlijke kwantumeffecten.
De wet van Planck heeft vele consequenties. Een ervan is dat de vorm van de kromme uitsluitend afhangt van het verwarmde lichaam en niet van het materiaal waarvan het gemaakt is. Daarom straalt de zon op dezelfde manier als een stuk metaal dat tot dezelfde temperatuur (5,800 K) verhit wordt.
We noemen ook de wet van Wien die stelt dat de maximale golflengte λMax omgekeerd evenredig is met de temperatuur:
λMax ∝ 1 / T
En de wet van Boltzmann die stelt dat het totaal uitgestraalde vermogen (per oppervlakte-eenheid) evenredig is met T4:
M = σ.T4

Discover EduMedia for free
The interactive encyclopedia that brings science and math to life in the classroom.
Over 1,000 resources





